La importancia de las ecuaciones matemáticas está en que permiten plantear y resolver innumerables problemas en diversas áreas: economía, ciencias sociales física, matemáticas, biología, ingeniería, química, astronomía, electrónica, aeronáutica, pero también ayudan a resolver problemas cotidianos.
En matemáticas, se denomina ecuación a la igualdad entre dos expresiones, en las cuales aparecen una o varias cantidades desconocidas llamadas incógnitas.
Las incógnitas, por lo general, están representadas por letras, y más precisamente, por la últimas letras del abecedario (u, v, x, y, z). Cuando estas adoptan ciertos valores, que cumplen o satisfacen la igualdad, se tiene una solución o raíz de la ecuación.
Puede darse el caso de que la ecuación no tenga ninguna solución, que tenga solo una (ecuación determinada), que tenga más de una o que tenga infinitas soluciones (ecuación indeterminada).
Son ejemplos de ecuaciones:
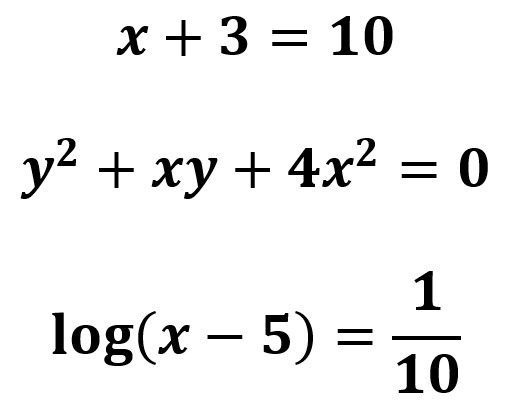
Para tener claro el concepto de ecuación es conveniente destacar lo siguiente:
1- No toda igualdad es una ecuación, por ejemplo: 9 x 3 = 27. Es una igualdad, pero, al no tener incógnita, no es una ecuación.
2- Cuando todos los posibles valores de una incógnita cumplen la igualdad, estamos en presencia de una identidad matemática (no de una ecuación). Expresiones como:
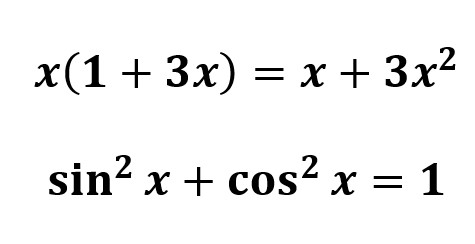
3- Tanto las identidades como las ecuaciones son igualdades, las primeras se satisfacen siempre, mientras que las ecuaciones solo se satisfacen para algunos valores (o puede que para ninguno).
Table of Contents
Elementos de una ecuación
En una ecuación matemática se distinguen los siguientes elementos:
Miembros. Son las dos expresiones matemáticas que están a cada lado del signo igual (=). Todo lo que está al lado izquierdo del signo igual se denomina primer miembro. Todo lo que aparece al lado derecho del signo igual es el segundo miembro.
Términos. Cada miembro está formado por uno o varios términos. Los términos que están en un mismo miembro están conectados con los operadores matemáticos de suma (+) o diferencia (-). Los términos pueden ser: constantes (en este caso particular se denominan términos independientes), variables, funciones, vectores, matrices.
Un miembro de una ecuación y un término son expresiones coincidentes cuando el miembro tiene un solo término.
Incógnitas. Como lo habíamos mencionado, son los valores desconocidos. Pueden ser valores numéricos (en las ecuaciones algebraicas y en las ecuaciones trascendentes) o funciones (en las ecuaciones funcionales, las diferenciales y las integrales).
Coeficientes. Son las cantidades que multiplican a los términos que contienen incógnitas.
Consideremos el siguiente ejemplo:
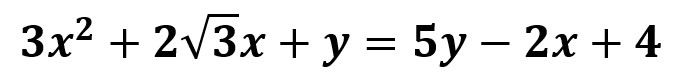
En esta ecuación aparecen dos incógnitas x e y.
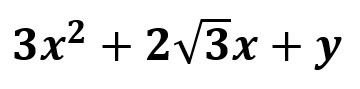
Está formado por 3 términos. El segundo miembro es:
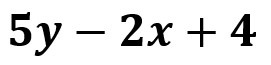
y tiene 3 términos.
Los números reales que acompañan las incógnitas son los coeficientes.
En este caso, lo coeficientes son:
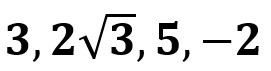
El número 4 es un término independiente.
Lectura Recomendada: Si no te gustan las matemáticas debes leer esto
Consideraciones para resolver ecuaciones
En la resolución de cualquier tipo de ecuación, conviene tener en cuenta que:
- Dos ecuaciones son equivalentes cuando tienen las mismas soluciones.
- Las ecuaciones satisfacen las propiedades fundamentales de las igualdades, a saber:
- Si sumamos o restamos una misma cantidad a ambos miembros de una ecuación, el resultado es una ecuación equivalente a la original.
- Si multiplicamos o dividimos ambos miembros de una ecuación por una constante distinta de cero, se obtiene como resultado otra ecuación que es equivalente a la primera.
Además:
- Cualquier término se puede cambiar de un miembro a otro de la ecuación, siguiendo la regla de transposición de términos, es decir, cambiando su signo.
- Se pueden suprimir de la ecuación los términos iguales con signos iguales que estén en distintos miembros.
- Todos los términos de una ecuación se pueden cambiar de signo de manera simultánea. Esto es lo mismo que multiplicar la ecuación por -1 .
Tipos de ecuaciones
Existen muchas formas de escribir una ecuación matemática, lo cual da origen a los diferentes tipos. Conocer el tipo de ecuación es el primer paso para buscar la solución de la misma.
Los dos tipos básicos de ecuaciones matemáticas son:
1- Ecuaciones numéricas:
se dividen en ecuaciones algebraicas y ecuaciones trascendentes.
2- Ecuaciones funcionales:
Entre las que se pueden mencionar las ecuaciones funcionales propiamente, las ecuaciones diferenciales y las ecuaciones integrales. Seguidamente se presenta una breve definición de cada una de ellas.
1- Ecuaciones algebraicas o polinómicas.
Son las ecuaciones matemáticas fundamentales. En ellas, ambos miembros son polinomios o se pueden reducir a un polinomio igualado a cero (forma canónica). También se incluyen en este tipo, las ecuaciones donde los polinomios se presentan en expresiones racionales o en radicales.
De estas ecuaciones tenemos varios tipos como se muestra a continuación.
1.1- Ecuaciones de primer grado o ecuaciones lineales
Son las que involucran una o más incógnitas a la primera potencia, sin que existan términos que multipliquen dos o más variables.
Su forma más sencilla es la ecuación con una sola incógnita
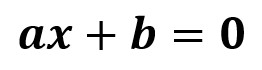
Donde a y b son números reales conocidos y a no es igual a 0. Esta ecuación tiene una única solución dada por:
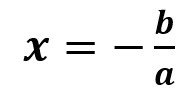
Muchas ecuaciones de primer grado se pueden presentar de forma distinta a la mostrada, pero a través de operaciones algebraicas y, con el uso de las propiedades de las igualdades es posible transformarlas a la ecuación indicada.
También podemos destacar entre este tipo de ecuaciones, las que presentan la forma
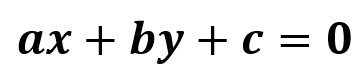
Con a, b y c números reales (a y b no se anulan simultáneamente). Esta ecuación representa una recta en el plano cartesiano. Todos los puntos que pertenecen a esta recta son soluciones o raíces de la ecuación, por lo tanto, esta ecuación tiene infinitas soluciones.
1.2- Ecuaciones de segundo grado o ecuaciones cuadráticas con una incógnita
Son ecuaciones que una vez simplificadas adquieren la forma
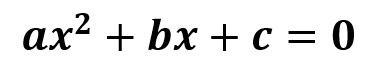
Donde los coeficientes a, b y c, son cantidades reales y conocidas y, además, a diferente a 0, ya que, si no, la ecuación no sería de segundo grado. Esta ecuación tiene como máximo dos soluciones.
Cuando los tres coeficientes son distintos de cero, se dice que es una ecuación de segundo grado completa. Cuando alguno de los coeficientes b o c o ambos son nulos, se dice que es una ecuación de segundo grado incompleta.
Se resuelven a partir de la ecuación general:
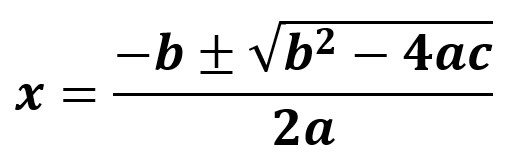
1.3- Ecuaciones de grado n con una incógnita
Las ecuaciones polinómicas de grado n tienen la forma general
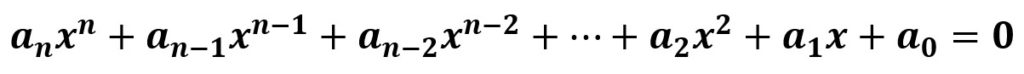
Los números reales son:
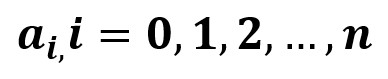
y
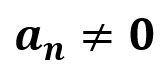
son números reales. El máximo exponente n, al que se encuentra elevada la incógnita es el grado de la ecuación e indica el número máximo de soluciones o raíces de la ecuación.
1.4- Ecuaciones bicuadradas
Son un tipo especial de ecuaciones de cuarto grado, en las cuales no aparecen los términos de grado impar, por lo que se reducen a la forma
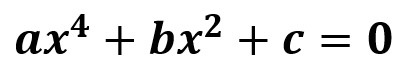
1.5- Ecuaciones racionales
Son aquellas en las que uno o ambos miembros de la ecuación se representan como el cociente de dos polinomios.
Es decir
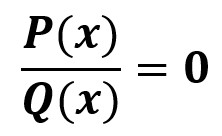
Por ejemplo:
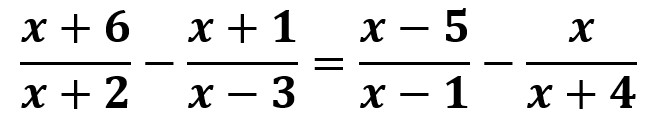
1.6- Ecuaciones irracionales
Son aquellas en las que, al menos, un polinomio aparece bajo el signo radical. Por ejemplo:
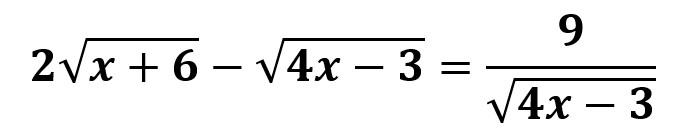
1.7- Ecuaciones diofánticas o diofantinas
Son ecuaciones algebraicas en las cuales los coeficientes de los términos pertenecen a los números naturales N , o a los números enteros Z. Y se consideran como soluciones únicamente las que pertenezcan a estos conjuntos de números.
2- Ecuaciones trascendentes
Son ecuaciones matemáticas que van más allá del álgebra y los polinomios, pues involucran funciones como las trigonométricas, logarítmicas y exponenciales. Aunque en general se les llama trascendentes, cuando involucran solo un tipo de función se les puede llamar:
2.1- Ecuaciones trigonométricas o goniométricas
La incógnita aparece al menos una vez como argumento de cualquiera de las funciones trigonométricas.
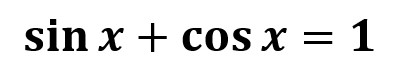
2.2- Ecuaciones logarítmicas
Se caracterizan porque la incógnita aparece como argumento de un logaritmo
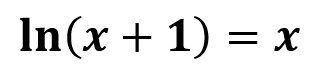
2.3- Ecuaciones exponenciales
En este tipo de ecuaciones las incógnitas aparecen como exponentes
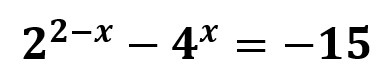
3– Ecuaciones funcionales
Son aquellas donde la incógnita es una función de una variable. Es decir, en lugar de un valor, la solución de la ecuación es una relación de dependencia de una variable con respecto a otras.
Este tipo de ecuaciones expresa una relación entre los valores de una función en algunos puntos de su dominio. Dicha relación se puede expresar por medio de operaciones como sumas, restas, multiplicaciones y divisiones, o por composición.
Se excluyen de esta clase las ecuaciones diferenciales e integrales, que, aunque son ecuaciones funcionales, se consideran otros tipos de ecuaciones.
Son ejemplos de ecuaciones funcionales
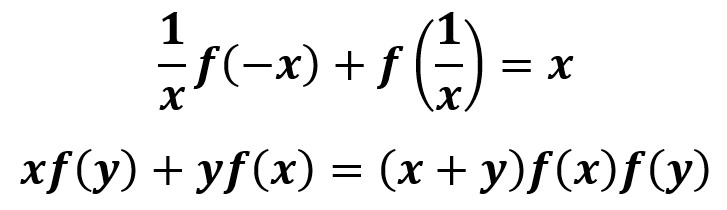
4- Ecuaciones diferenciales
Son ecuaciones donde aparecen las derivadas de una o varias funciones de las variables (incógnitas) desconocidas. Tienen un amplio uso en la física, ingeniería y ciencias técnicas, donde las magnitudes varían constantemente, por lo que se consideran las ecuaciones matemáticas funcionales más importantes y son una herramienta poderosa para la investigación. Pueden ser clasificadas como:
4.1- Ecuaciones diferenciales ordinarias
Cuando aparecen una o más derivadas de solo una función desconocida de una de las variables. En este caso, el orden de la derivada máxima es también el orden de la ecuación. Por lo tanto, tenemos ecuaciones diferenciales ordinarias de primer orden, de segundo orden, etc.
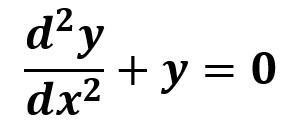
4.2- Ecuaciones en derivadas parciales
Son ecuaciones cuyas incógnitas son funciones de varias variables y en ellas aparecen tanto las funciones como sus derivadas parciales. Supongamos, por ejemplo, la ecuación
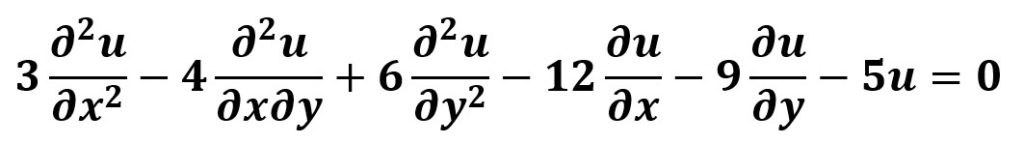
Cuya incógnita es la función u(x,y).
Otra forma de clasificar las ecuaciones diferenciales es:
- Lineales, cuando la máxima potencia de las derivadas y de la función es uno y, además, no existen términos donde la función desconocida multiplique a sus derivadas.
- No lineales, en otro caso.
5- Ecuaciones integrales
En las ecuaciones integrales, la incógnita aparece dentro de una operación integral.
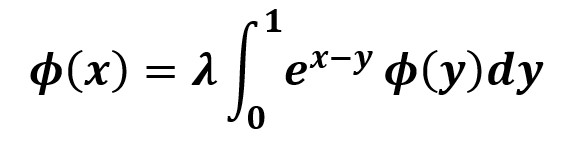
Estas ecuaciones se dividen en Ecuaciones de Volterra y Ecuaciones de Fredholm, atendiendo a los métodos que se utilizan para estudiarlas.












0 comentarios